Modeling Examples¶
This chapter includes commented examples on modeling and solving optimization problems with Python-MIP.
The 0/1 Knapsack Problem¶
As a first example, consider the solution of the 0/1 knapsack problem: given a set \(I\) of items, each one with a weight \(w_i\) and estimated profit \(p_i\), one wants to select a subset with maximum profit such that the summation of the weights of the selected items is less or equal to the knapsack capacity \(c\). Considering a set of decision binary variables \(x_i\) that receive value 1 if the \(i\)-th item is selected, or 0 if not, the resulting mathematical programming formulation is:
The following python code creates, optimizes and prints the optimal solution for the 0/1 knapsack problem
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | from mip import Model, xsum, maximize, BINARY
p = [10, 13, 18, 31, 7, 15]
w = [11, 15, 20, 35, 10, 33]
c, I = 47, range(len(w))
m = Model("knapsack")
x = [m.add_var(var_type=BINARY) for i in I]
m.objective = maximize(xsum(p[i] * x[i] for i in I))
m += xsum(w[i] * x[i] for i in I) <= c
m.optimize()
selected = [i for i in I if x[i].x >= 0.99]
print("selected items: {}".format(selected))
|
Line 3 imports the required classes and definitions from Python-MIP. Lines 5-8 define the problem data. Line 10 creates an empty maximization
problem m with the (optional) name of “knapsack”. Line 12 adds the binary decision variables to model m and stores their references in a list x. Line 14 defines the objective function of this model and line 16 adds the capacity constraint. The model is optimized in line 18 and the solution, a list of the selected
items, is computed at line 20.
The Traveling Salesman Problem¶
The traveling salesman problem (TSP) is one of the most studied combinatorial optimization problems, with the first computational studies dating back to the 50s [Dantz54], [Appleg06]. To to illustrate this problem, consider that you will spend some time in Belgium and wish to visit some of its main tourist attractions, depicted in the map bellow:
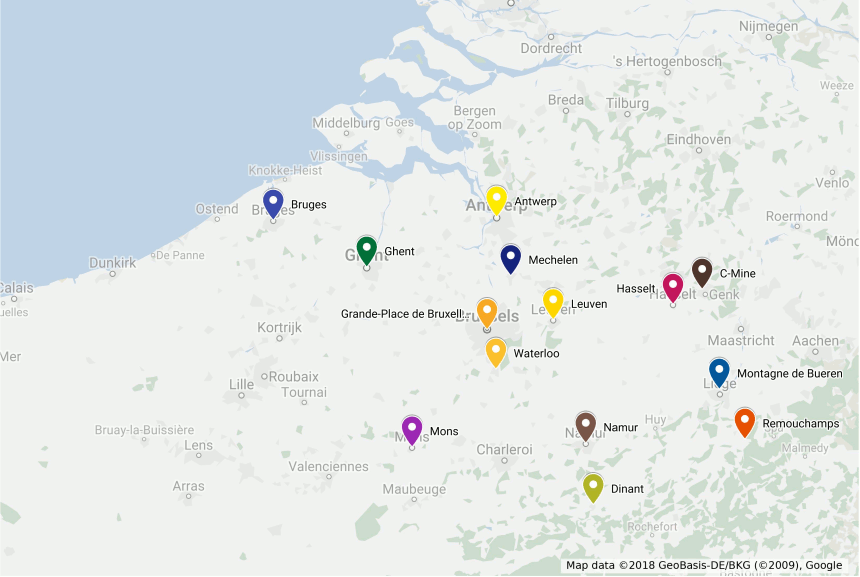
You want to find the shortest possible tour to visit all these places. More formally, considering \(n\) points \(V=\{0,\ldots,n-1\}\) and a distance matrix \(D_{n \times n}\) with elements \(c_{i,j} \in \mathbb{R}^+\), a solution consists in a set of exactly \(n\) (origin, destination) pairs indicating the itinerary of your trip, resulting in the following formulation:
The first two sets of constraints enforce that we leave and arrive only once at each point. The optimal solution for the problem including only these constraints could result in a solution with sub-tours, such as the one bellow.
To enforce the production of connected routes, additional variables \(y_{i} \geq 0\) are included in the model indicating the sequential order of each point in the produced route. Point zero is arbitrarily selected as the initial point and conditional constraints linking variables \(x_{i,j}\), \(y_{i}\) and \(y_{j}\) are created for all nodes except the the initial one to ensure that the selection of the arc \(x_{i,j}\) implies that \(y_{j}\geq y_{i}+1\).
The Python code to create, optimize and print the optimal route for the TSP is included bellow:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 | from itertools import product
from sys import stdout as out
from mip import Model, xsum, minimize, BINARY
# names of places to visit
places = ['Antwerp', 'Bruges', 'C-Mine', 'Dinant', 'Ghent',
'Grand-Place de Bruxelles', 'Hasselt', 'Leuven',
'Mechelen', 'Mons', 'Montagne de Bueren', 'Namur',
'Remouchamps', 'Waterloo']
# distances in an upper triangular matrix
dists = [[83, 81, 113, 52, 42, 73, 44, 23, 91, 105, 90, 124, 57],
[161, 160, 39, 89, 151, 110, 90, 99, 177, 143, 193, 100],
[90, 125, 82, 13, 57, 71, 123, 38, 72, 59, 82],
[123, 77, 81, 71, 91, 72, 64, 24, 62, 63],
[51, 114, 72, 54, 69, 139, 105, 155, 62],
[70, 25, 22, 52, 90, 56, 105, 16],
[45, 61, 111, 36, 61, 57, 70],
[23, 71, 67, 48, 85, 29],
[74, 89, 69, 107, 36],
[117, 65, 125, 43],
[54, 22, 84],
[60, 44],
[97],
[]]
# number of nodes and list of vertices
n, V = len(dists), set(range(len(dists)))
# distances matrix
c = [[0 if i == j
else dists[i][j-i-1] if j > i
else dists[j][i-j-1]
for j in V] for i in V]
model = Model()
# binary variables indicating if arc (i,j) is used on the route or not
x = [[model.add_var(var_type=BINARY) for j in V] for i in V]
# continuous variable to prevent subtours: each city will have a
# different sequential id in the planned route except the first one
y = [model.add_var() for i in V]
# objective function: minimize the distance
model.objective = minimize(xsum(c[i][j]*x[i][j] for i in V for j in V))
# constraint : leave each city only once
for i in V:
model += xsum(x[i][j] for j in V - {i}) == 1
# constraint : enter each city only once
for i in V:
model += xsum(x[j][i] for j in V - {i}) == 1
# subtour elimination
for (i, j) in product(V - {0}, V - {0}):
if i != j:
model += y[i] - (n+1)*x[i][j] >= y[j]-n
# optimizing
model.optimize()
# checking if a solution was found
if model.num_solutions:
out.write('route with total distance %g found: %s'
% (model.objective_value, places[0]))
nc = 0
while True:
nc = [i for i in V if x[nc][i].x >= 0.99][0]
out.write(' -> %s' % places[nc])
if nc == 0:
break
out.write('\n')
|
In line 10 names of the places to visit are informed. In line 17 distances are informed in an upper triangular matrix. Line 33 stores the number of nodes and a list with nodes sequential ids starting from 0. In line 36 a full \(n \times n\) distance matrix is filled. Line 41 creates an empty MIP model. In line 44 all binary decision variables for the selection of arcs are created and their references are stored a \(n \times n\) matrix named x. Differently from the \(x\) variables, \(y\) variables (line 48) are not required to be
binary or integral, they can be declared just as continuous variables, the default variable type. In this case, the parameter var_type can be omitted from the add_var call.
Line 51 sets the total traveled distance as objective function and lines 54-62 include the constraints. In line 66 we call the optimizer specifying a time limit of 30 seconds. This
will surely not be necessary for our Belgium example, which will be solved instantly, but may be important for larger problems: even though high quality solutions may be found very quickly by the MIP solver, the time required to prove that the current solution is optimal may be very
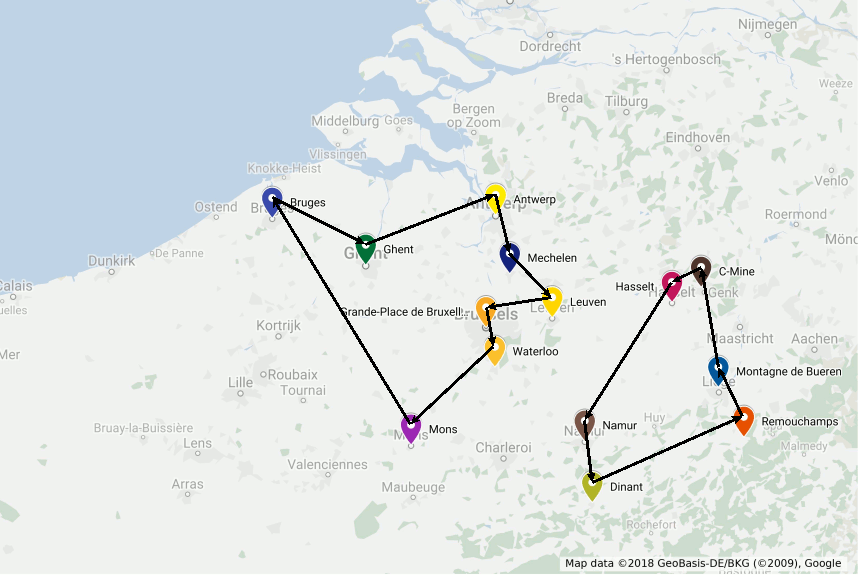
large. With a time limit, the search is truncated and the best solution found during the search is reported. In line 69 we check for the availability of a feasible solution. To repeatedly check for the next node in the route we check for the solution value (.x attribute) of all variables of outgoing arcs of the current node in the route (line 73). The optimal solution for our trip has length 547 and is depicted bellow:

n-Queens¶
In the \(n\)-queens puzzle \(n\) chess queens should to be placed in a board with \(n\times n\) cells in a way that no queen can attack another, i.e., there must be at most one queen per row, column and diagonal. This is a constraint satisfaction problem: any feasible solution is acceptable and no objective function is defined. The following binary programming formulation can be used to solve this problem:
The following code builds the previous model, solves it and prints the queen placements:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | from sys import stdout
from mip import Model, xsum, BINARY
# number of queens
n = 40
queens = Model()
x = [[queens.add_var('x({},{})'.format(i, j), var_type=BINARY)
for j in range(n)] for i in range(n)]
# one per row
for i in range(n):
queens += xsum(x[i][j] for j in range(n)) == 1, 'row({})'.format(i)
# one per column
for j in range(n):
queens += xsum(x[i][j] for i in range(n)) == 1, 'col({})'.format(j)
# diagonal \
for p, k in enumerate(range(2 - n, n - 2 + 1)):
queens += xsum(x[i][i - k] for i in range(n)
if 0 <= i - k < n) <= 1, 'diag1({})'.format(p)
# diagonal /
for p, k in enumerate(range(3, n + n)):
queens += xsum(x[i][k - i] for i in range(n)
if 0 <= k - i < n) <= 1, 'diag2({})'.format(p)
queens.optimize()
if queens.num_solutions:
stdout.write('\n')
for i, v in enumerate(queens.vars):
stdout.write('O ' if v.x >= 0.99 else '. ')
if i % n == n-1:
stdout.write('\n')
|
Frequency Assignment¶
The design of wireless networks, such as cell phone networks, involves assigning communication frequencies to devices. These communication frequencies can be separated into channels. The geographical area covered by a network can be divided into hexagonal cells, where each cell has a base station that covers a given area. Each cell requires a different number of channels, based on usage statistics and each cell has a set of neighbor cells, based on the geographical distances. The design of an efficient mobile network involves selecting subsets of channels for each cell, avoiding interference between calls in the same cell and in neighboring cells. Also, for economical reasons, the total bandwidth in use must be minimized, i.e., the total number of different channels used. One of the first real cases discussed in literature are the Philadelphia [Ande73] instances, with the structure depicted bellow:
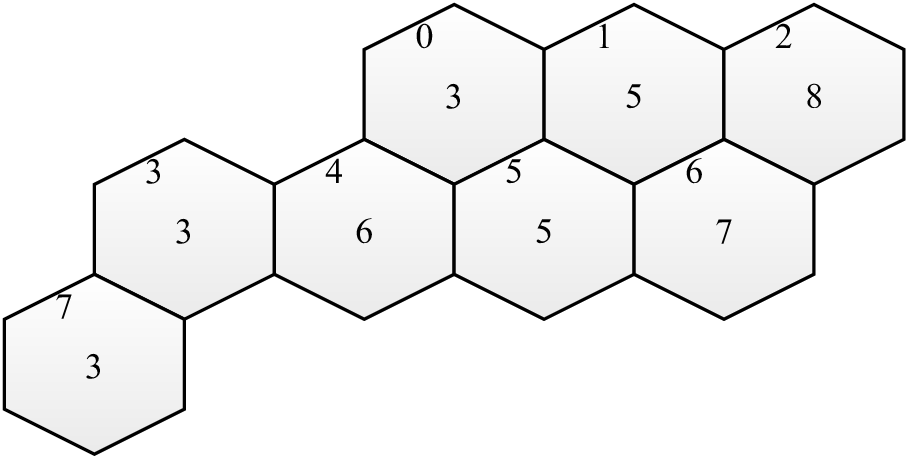
Each cell has a demand with the required number of channels drawn at the center of the hexagon, and a sequential id at the top left corner. Also, in this example, each cell has a set of at most 6 adjacent neighboring cells (distance 1). The largest demand (8) occurs on cell 2. This cell has the following adjacent cells, with distance 1: (1, 6). The minimum distances between channels in the same cell in this example is 3 and channels in neighbor cells should differ by at least 2 units.
A generalization of this problem (not restricted to the hexagonal topology), is the Bandwidth Multicoloring Problem (BMCP), which has the following input data:
- \(N\):
set of cells, numbered from 1 to \(n\);
- \(r_i \in \mathbb{Z}^+\):
demand of cell \(i \in N\), i.e., the required number of channels;
- \(d_{i,j} \in \mathbb{Z}^+\):
minimum distance between channels assigned to nodes \(i\) and \(j\), \(d_{i,i}\) indicates the minimum distance between different channels allocated to the same cell.
Given an upper limit \(\overline{u}\) on the maximum number of channels \(U=\{1,\ldots,\overline{u}\}\) used, which can be obtained using a simple greedy heuristic, the BMPC can be formally stated as the combinatorial optimization problem of defining subsets of channels \(C_1, \ldots, C_n\) while minimizing the used bandwidth and avoiding interference:
This problem can be formulated as a mixed integer program with binary variables indicating the composition of the subsets: binary variables \(x_{(i,c)}\) indicate if for a given cell \(i\) channel \(c\) is selected (\(x_{(i,c)}=1\)) or not (\(x_{(i,c)}=0\)). The BMCP can be modeled with the following MIP formulation:
Follows the example of a solver for the BMCP using the previous MIP formulation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | from itertools import product
from mip import Model, xsum, minimize, BINARY
# number of channels per node
r = [3, 5, 8, 3, 6, 5, 7, 3]
# distance between channels in the same node (i, i) and in adjacent nodes
# 0 1 2 3 4 5 6 7
d = [[3, 2, 0, 0, 2, 2, 0, 0], # 0
[2, 3, 2, 0, 0, 2, 2, 0], # 1
[0, 2, 3, 0, 0, 0, 3, 0], # 2
[0, 0, 0, 3, 2, 0, 0, 2], # 3
[2, 0, 0, 2, 3, 2, 0, 0], # 4
[2, 2, 0, 0, 2, 3, 2, 0], # 5
[0, 2, 2, 0, 0, 2, 3, 0], # 6
[0, 0, 0, 2, 0, 0, 0, 3]] # 7
N = range(len(r))
# in complete applications this upper bound should be obtained from a feasible
# solution produced with some heuristic
U = range(sum(d[i][j] for (i, j) in product(N, N)) + sum(el for el in r))
m = Model()
x = [[m.add_var('x({},{})'.format(i, c), var_type=BINARY)
for c in U] for i in N]
z = m.add_var('z')
m.objective = minimize(z)
for i in N:
m += xsum(x[i][c] for c in U) == r[i]
for i, j, c1, c2 in product(N, N, U, U):
if i != j and c1 <= c2 < c1+d[i][j]:
m += x[i][c1] + x[j][c2] <= 1
for i, c1, c2 in product(N, U, U):
if c1 < c2 < c1+d[i][i]:
m += x[i][c1] + x[i][c2] <= 1
for i, c in product(N, U):
m += z >= (c+1)*x[i][c]
m.optimize(max_nodes=30)
if m.num_solutions:
for i in N:
print('Channels of node %d: %s' % (i, [c for c in U if x[i][c].x >=
0.99]))
|
Resource Constrained Project Scheduling¶
The Resource-Constrained Project Scheduling Problem (RCPSP) is a combinatorial optimization problem that consists of finding a feasible scheduling for a set of \(n\) jobs subject to resource and precedence constraints. Each job has a processing time, a set of successors jobs and a required amount of different resources. Resources may be scarce but are renewable at each time period. Precedence constraints between jobs mean that no jobs may start before all its predecessors are completed. The jobs must be scheduled non-preemptively, i.e., once started, their processing cannot be interrupted.
The RCPSP has the following input data:
- \(\mathcal{J}\)
jobs set
- \(\mathcal{R}\)
renewable resources set
- \(\mathcal{S}\)
set of precedences between jobs \((i,j) \in \mathcal{J} \times \mathcal{J}\)
- \(\mathcal{T}\)
planning horizon: set of possible processing times for jobs
- \(p_{j}\)
processing time of job \(j\)
- \(u_{(j,r)}\)
amount of resource \(r\) required for processing job \(j\)
- \(c_r\)
capacity of renewable resource \(r\)
In addition to the jobs that belong to the project, the set \(\mathcal{J}\) contains jobs \(0\) and \(n+1\), which are dummy jobs that represent the beginning and the end of the planning, respectively. The processing time for the dummy jobs is always zero and these jobs do not consume resources.
A binary programming formulation was proposed by Pritsker et al. [PWW69]. In this formulation, decision variables \(x_{jt} = 1\) if job \(j\) is assigned to begin at time \(t\); otherwise, \(x_{jt} = 0\). All jobs must finish in a single instant of time without violating precedence constraints while respecting the amount of available resources. The model proposed by Pristker can be stated as follows:
An instance is shown below. The figure shows a graph where jobs in \(\mathcal{J}\) are represented by nodes and precedence relations \(\mathcal{S}\) are represented by directed edges. The time-consumption \(p_{j}\) and all information concerning resource consumption \(u_{(j,r)}\) are included next to the graph. This instance contains 10 jobs and 2 renewable resources, \(\mathcal{R}=\{r_{1}, r_{2}\}\), where \(c_{1}\) = 6 and \(c_{2}\) = 8. Finally, a valid (but weak) upper bound on the time horizon \(\mathcal{T}\) can be estimated by summing the duration of all jobs.
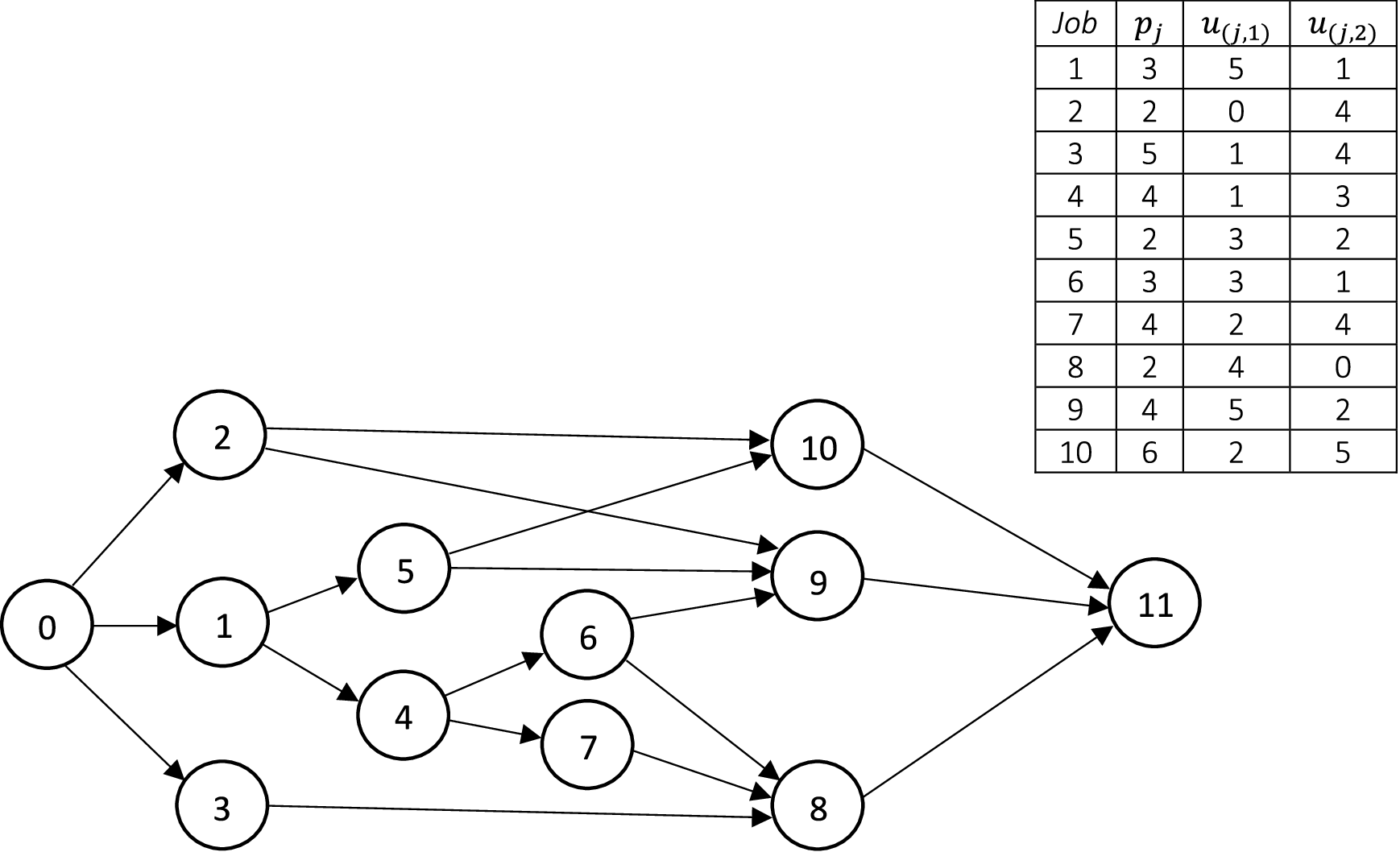
The Python code for creating the binary programming model, optimize it and print the optimal scheduling for RCPSP is included below:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | from itertools import product
from mip import Model, xsum, BINARY
n = 10 # note there will be exactly 12 jobs (n=10 jobs plus the two 'dummy' ones)
p = [0, 3, 2, 5, 4, 2, 3, 4, 2, 4, 6, 0]
u = [[0, 0], [5, 1], [0, 4], [1, 4], [1, 3], [3, 2], [3, 1], [2, 4],
[4, 0], [5, 2], [2, 5], [0, 0]]
c = [6, 8]
S = [[0, 1], [0, 2], [0, 3], [1, 4], [1, 5], [2, 9], [2, 10], [3, 8], [4, 6],
[4, 7], [5, 9], [5, 10], [6, 8], [6, 9], [7, 8], [8, 11], [9, 11], [10, 11]]
(R, J, T) = (range(len(c)), range(len(p)), range(sum(p)))
model = Model()
x = [[model.add_var(name="x({},{})".format(j, t), var_type=BINARY) for t in T] for j in J]
model.objective = xsum(t * x[n + 1][t] for t in T)
for j in J:
model += xsum(x[j][t] for t in T) == 1
for (r, t) in product(R, T):
model += (
xsum(u[j][r] * x[j][t2] for j in J for t2 in range(max(0, t - p[j] + 1), t + 1))
<= c[r])
for (j, s) in S:
model += xsum(t * x[s][t] - t * x[j][t] for t in T) >= p[j]
model.optimize()
print("Schedule: ")
for (j, t) in product(J, T):
if x[j][t].x >= 0.99:
print("Job {}: begins at t={} and finishes at t={}".format(j, t, t+p[j]))
print("Makespan = {}".format(model.objective_value))
|
One optimum solution is shown bellow, from the viewpoint of resource consumption.
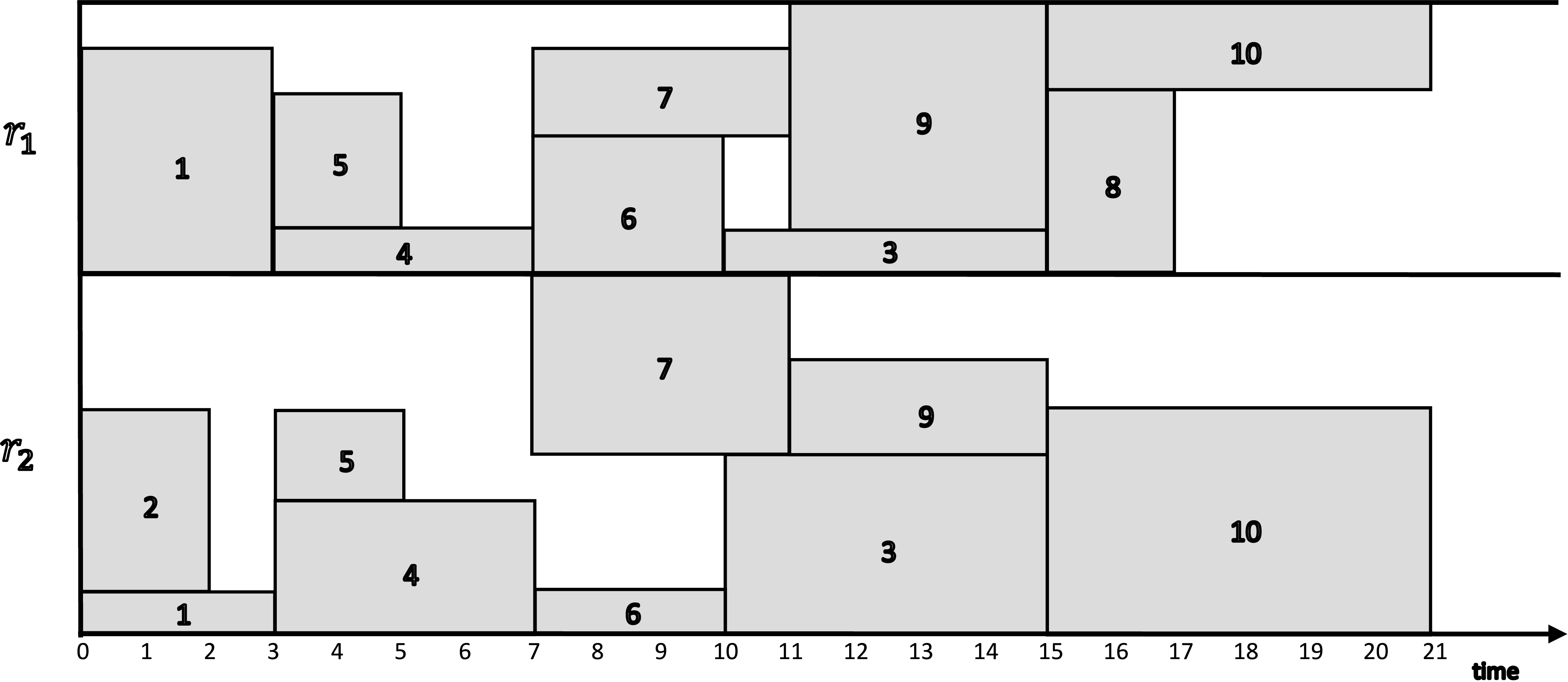
It is noteworthy that this particular problem instance has multiple optimal solutions. Keep in the mind that the solver may obtain a different optimum solution.
Job Shop Scheduling Problem¶
The Job Shop Scheduling Problem (JSSP) is an NP-hard problem defined by a set of jobs that must be executed by a set of machines in a specific order for each job. Each job has a defined execution time for each machine and a defined processing order of machines. Also, each job must use each machine only once. The machines can only execute a job at a time and once started, the machine cannot be interrupted until the completion of the assigned job. The objective is to minimize the makespan, i.e. the maximum completion time among all jobs.
For instance, suppose we have 3 machines and 3 jobs. The processing order for each job is as follows (the processing time of each job in each machine is between parenthesis):
Job \(j_1\): \(m_3\) (2) \(\rightarrow\) \(m_1\) (1) \(\rightarrow\) \(m_2\) (2)
Job \(j_2\): \(m_2\) (1) \(\rightarrow\) \(m_3\) (2) \(\rightarrow\) \(m_1\) (2)
Job \(j_3\): \(m_3\) (1) \(\rightarrow\) \(m_2\) (2) \(\rightarrow\) \(m_1\) (1)
Bellow there are two feasible schedules:
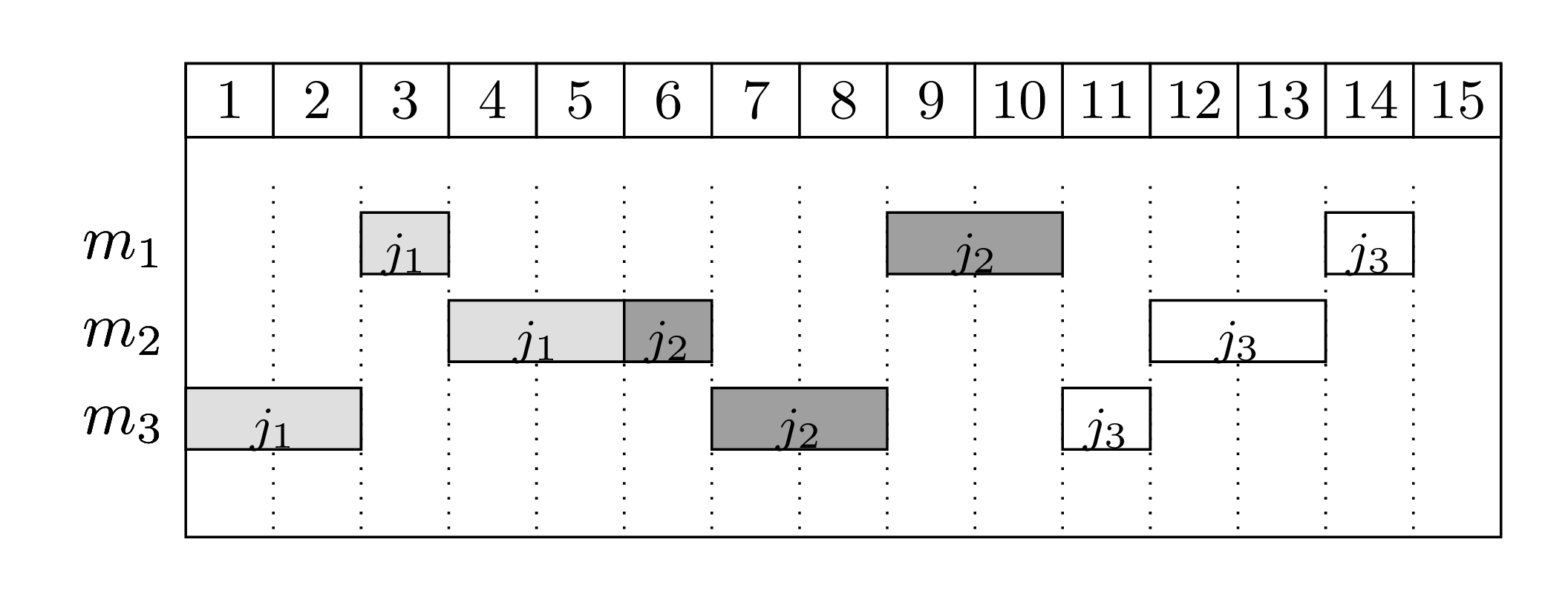
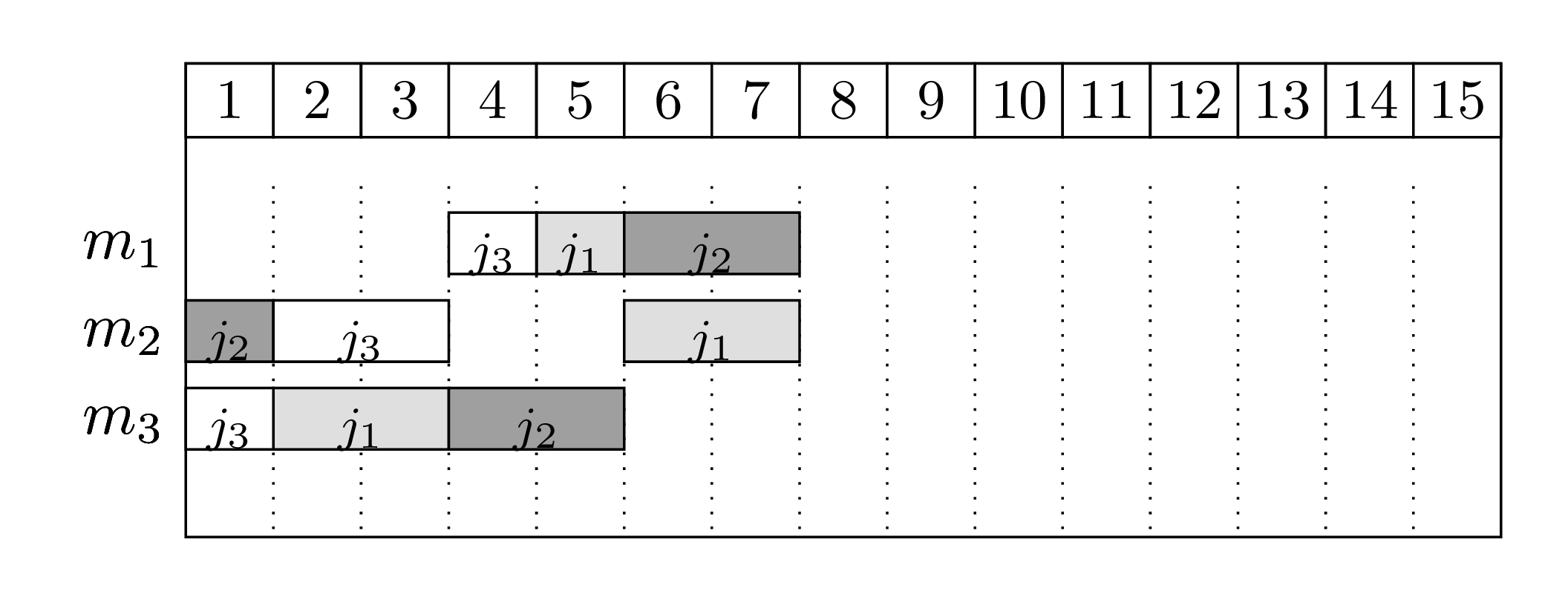
The first schedule shows a naive solution: jobs are processed in a sequence and machines stay idle quite often. The second solution is the optimal one, where jobs execute in parallel.
The JSSP has the following input data:
- \(\mathcal{J}\)
set of jobs, \(\mathcal{J} = \{1,...,n\}\),
- \(\mathcal{M}\)
set of machines, \(\mathcal{M} = \{1,...,m\}\),
- \(o^j_r\)
the machine that processes the \(r\)-th operation of job \(j\), the sequence without repetition \(O^j = (o^j_1,o^j_2,...,o^j_m)\) is the processing order of \(j\),
- \(p_{ij}\)
non-negative integer processing time of job \(j\) in machine \(i\).
A JSSP solution must respect the following constraints:
All jobs \(j\) must be executed following the sequence of machines given by \(O^j\),
Each machine can process only one job at a time,
Once a machine starts a job, it must be completed without interruptions.
The objective is to minimize the makespan, the end of the last job to be executed. The JSSP is NP-hard for any fixed \(n \ge 3\) and also for any fixed \(m \ge 3\).
The decision variables are defined by:
- \(x_{ij}\)
starting time of job \(j \in J\) on machine \(i \in M\)
- \(y_{ijk}=\)
\(\begin{cases} 1, & \text{if job } j \text{ precedes job } k \text{ on machine } i \text{,}\\ & i \in \mathcal{M} \text{, } j, k \in \mathcal{J} \text{, } j \neq k \\ 0, & \text{otherwise} \end{cases}\)
- \(C\)
variable for the makespan
Follows a MIP formulation [Mann60] for the JSSP. The objective function is computed in the auxiliary variable \(C\). The first set of constraints are the precedence constraints, that ensure that a job on a machine only starts after the processing of the previous machine concluded. The second and third set of disjunctive constraints ensure that only one job is processing at a given time in a given machine. The \(M\) constant must be large enough to ensure the correctness of these constraints. A valid (but weak) estimate for this value can be the summation of all processing times. The fourth set of constrains ensure that the makespan value is computed correctly and the last constraints indicate variable domains.
The following Python-MIP code creates the previous formulation, optimizes it and prints the optimal solution found:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | from itertools import product
from mip import Model, BINARY
n = m = 3
times = [[2, 1, 2],
[1, 2, 2],
[1, 2, 1]]
M = sum(times[i][j] for i in range(n) for j in range(m))
machines = [[2, 0, 1],
[1, 2, 0],
[2, 1, 0]]
model = Model('JSSP')
c = model.add_var(name="C")
x = [[model.add_var(name='x({},{})'.format(j+1, i+1))
for i in range(m)] for j in range(n)]
y = [[[model.add_var(var_type=BINARY, name='y({},{},{})'.format(j+1, k+1, i+1))
for i in range(m)] for k in range(n)] for j in range(n)]
model.objective = c
for (j, i) in product(range(n), range(1, m)):
model += x[j][machines[j][i]] - x[j][machines[j][i-1]] >= \
times[j][machines[j][i-1]]
for (j, k) in product(range(n), range(n)):
if k != j:
for i in range(m):
model += x[j][i] - x[k][i] + M*y[j][k][i] >= times[k][i]
model += -x[j][i] + x[k][i] - M*y[j][k][i] >= times[j][i] - M
for j in range(n):
model += c - x[j][machines[j][m - 1]] >= times[j][machines[j][m - 1]]
model.optimize()
print("Completion time: ", c.x)
for (j, i) in product(range(n), range(m)):
print("task %d starts on machine %d at time %g " % (j+1, i+1, x[j][i].x))
|
Cutting Stock / One-dimensional Bin Packing Problem¶
The One-dimensional Cutting Stock Problem (also often referred to as One-dimensional Bin Packing Problem) is an NP-hard problem first studied by Kantorovich in 1939 [Kan60]. The problem consists of deciding how to cut a set of pieces out of a set of stock materials (paper rolls, metals, etc.) in a way that minimizes the number of stock materials used.
[Kan60] proposed an integer programming formulation for the problem, given below:
This formulation can be improved by including symmetry reducing constraints, such as:
The following Python-MIP code creates the formulation proposed by [Kan60], optimizes it and prints the optimal solution found.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | from mip import Model, xsum, BINARY, INTEGER
n = 10 # maximum number of bars
L = 250 # bar length
m = 4 # number of requests
w = [187, 119, 74, 90] # size of each item
b = [1, 2, 2, 1] # demand for each item
# creating the model
model = Model()
x = {(i, j): model.add_var(obj=0, var_type=INTEGER, name="x[%d,%d]" % (i, j))
for i in range(m) for j in range(n)}
y = {j: model.add_var(obj=1, var_type=BINARY, name="y[%d]" % j)
for j in range(n)}
# constraints
for i in range(m):
model.add_constr(xsum(x[i, j] for j in range(n)) >= b[i])
for j in range(n):
model.add_constr(xsum(w[i] * x[i, j] for i in range(m)) <= L * y[j])
# additional constraints to reduce symmetry
for j in range(1, n):
model.add_constr(y[j - 1] >= y[j])
# optimizing the model
model.optimize()
# printing the solution
print('')
print('Objective value: {model.objective_value:.3}'.format(**locals()))
print('Solution: ', end='')
for v in model.vars:
if v.x > 1e-5:
print('{v.name} = {v.x}'.format(**locals()))
print(' ', end='')
|
Note in the code above that argument obj was employed to create the variables (see lines 11 and 13). By setting obj to a value different than zero, the created variable is automatically added to the objective function with coefficient equal to obj’s value.
Two-Dimensional Level Packing¶
In some industries, raw material must be cut in several pieces of specified size. Here we consider the case where these pieces are rectangular [LMM02]. Also, due to machine operation constraints, pieces should be grouped horizontally such that firstly, horizontal layers are cut with the height of the largest item in the group and secondly, these horizontal layers are then cut according to items widths. Raw material is provided in rolls with large height. To minimize waste, a given batch of items must be cut using the minimum possible total height to minimize waste.
Formally, the following input data defines an instance of the Two Dimensional Level Packing Problem (TDLPP):
- \(W\)
raw material width
- \(n\)
number of items
- \(I\)
set of items = \(\{0, \ldots, n-1\}\)
- \(w_i\)
width of item \(i\)
- \(h_i\)
height of item \(i\)
The following image illustrate a sample instance of the two dimensional level packing problem.
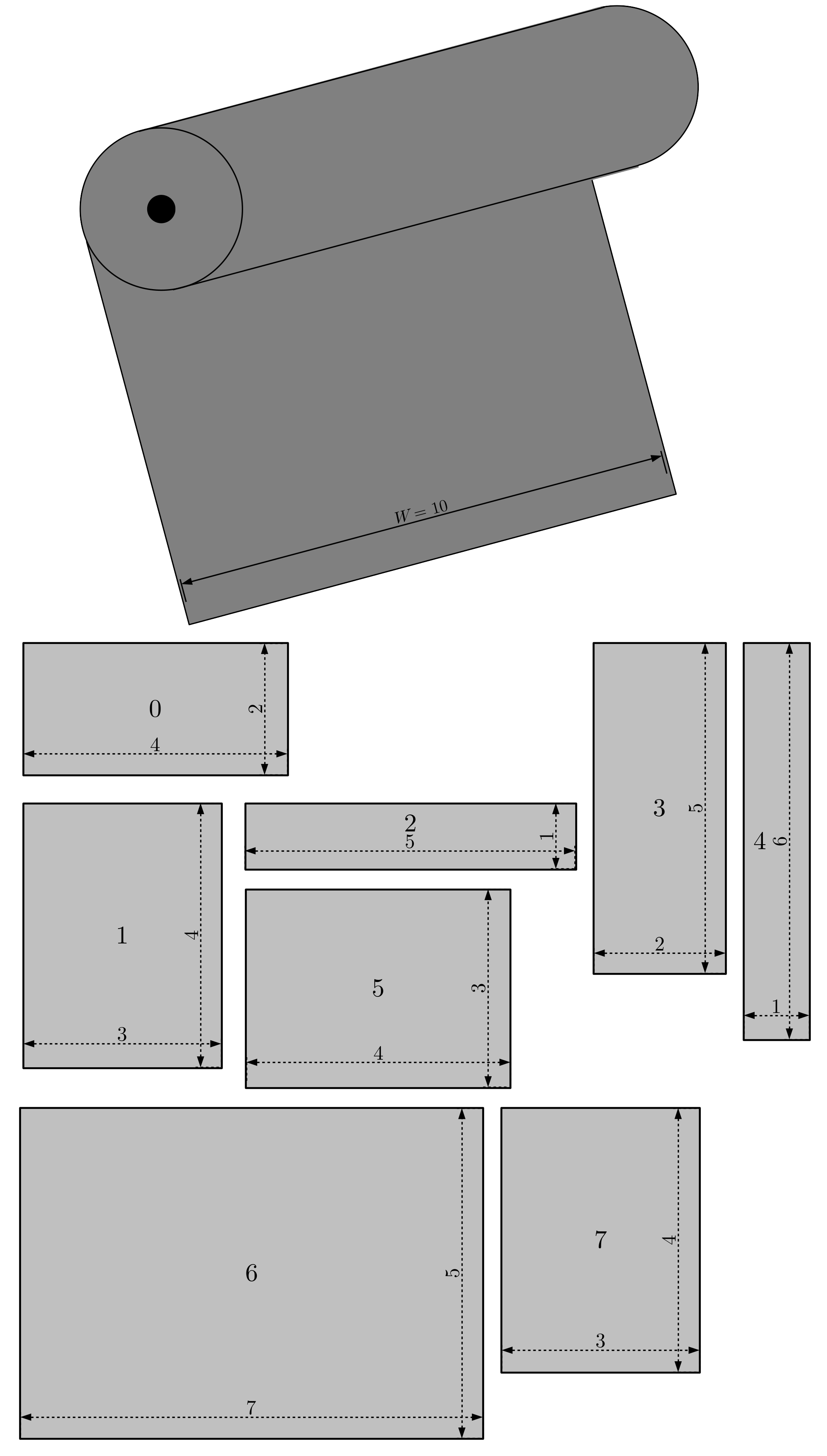
This problem can be formulated using binary variables \(x_{i,j} \in \{0, 1\}\), that indicate if item \(j\) should be grouped with item \(i\) (\(x_{i,j}=1\)) or not (\(x_{i,j}=0\)). Inside the same group, all elements should be linked to the largest element of the group, the representative of the group. If element \(i\) is the representative of the group, then \(x_{i,i}=1\).
Before presenting the complete formulation, we introduce two sets to simplify the notation. \(S_i\) is the set of items with width equal or smaller to item \(i\), i.e., items for which item \(i\) can be the representative item. Conversely, \(G_i\) is the set of items with width greater or equal to the width of \(i\), i.e., items which can be the representative of item \(i\) in a solution. More formally, \(S_i = \{j \in I : h_j \leq h_i\}\) and \(G_i = \{j \in I : h_j \geq h_i\}\). Note that both sets include the item itself.
The first constraints enforce that each item needs to be packed as the largest item of the set or to be included in the set of another item with width at least as large. The second set of constraints indicates that if an item is chosen as representative of a set, then the total width of the items packed within this same set should not exceed the width of the roll.
The following Python-MIP code creates and optimizes a model to solve the two-dimensional level packing problem illustrated in the previous figure.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | from mip import Model, BINARY, minimize, xsum
# 0 1 2 3 4 5 6 7
w = [4, 3, 5, 2, 1, 4, 7, 3] # widths
h = [2, 4, 1, 5, 6, 3, 5, 4] # heights
n = len(w)
I = set(range(n))
S = [[j for j in I if h[j] <= h[i]] for i in I]
G = [[j for j in I if h[j] >= h[i]] for i in I]
# raw material width
W = 10
m = Model()
x = [{j: m.add_var(var_type=BINARY) for j in S[i]} for i in I]
m.objective = minimize(xsum(h[i] * x[i][i] for i in I))
# each item should appear as larger item of the level
# or as an item which belongs to the level of another item
for i in I:
m += xsum(x[j][i] for j in G[i]) == 1
# represented items should respect remaining width
for i in I:
m += xsum(w[j] * x[i][j] for j in S[i] if j != i) <= (W - w[i]) * x[i][i]
m.optimize()
for i in [j for j in I if x[j][j].x >= 0.99]:
print(
"Items grouped with {} : {}".format(
i, [j for j in S[i] if i != j and x[i][j].x >= 0.99]
)
)
|
Plant Location with Non-Linear Costs¶
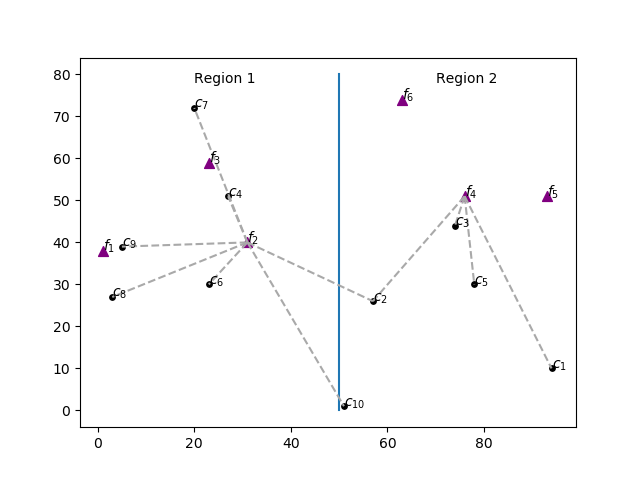
One industry plans to install two plants, one to the west (region 1) and another to the east (region 2). It must decide also the production capacity of each plant and allocate clients with different demands to plants in order to minimize shipping costs, which depend on the distance to the selected plant. Clients can be served by facilities of both regions. The cost of installing a plant with capacity \(z\) is \(f(z)=1520 \log z\). The Figure below shows the distribution of clients in circles and possible plant locations as triangles.
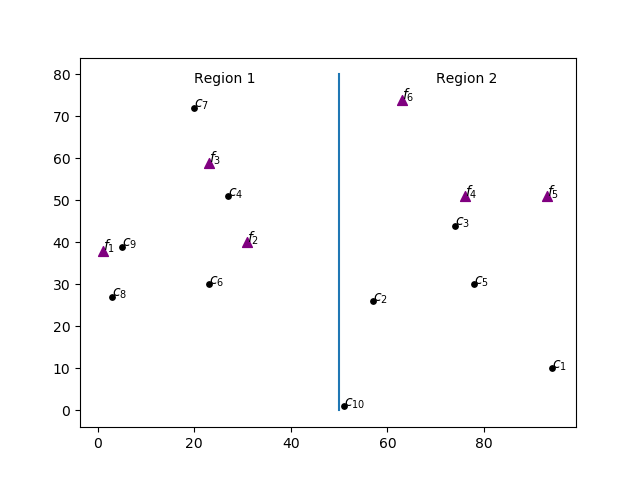
This example illustrates the use of Special Ordered Sets (SOS). We’ll use Type 1 SOS to ensure that only one of the plants in each region has a non-zero production capacity. The cost \(f(z)\) of building a plant with capacity \(z\) grows according to the non-linear function \(f(z)=1520 \log z\). Type 2 SOS will be used to model the cost of installing each one of the plants in auxiliary variables \(y\).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 | import matplotlib.pyplot as plt
from math import sqrt, log
from itertools import product
from mip import Model, xsum, minimize, OptimizationStatus
# possible plants
F = [1, 2, 3, 4, 5, 6]
# possible plant installation positions
pf = {1: (1, 38), 2: (31, 40), 3: (23, 59), 4: (76, 51), 5: (93, 51), 6: (63, 74)}
# maximum plant capacity
c = {1: 1955, 2: 1932, 3: 1987, 4: 1823, 5: 1718, 6: 1742}
# clients
C = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# position of clients
pc = {1: (94, 10), 2: (57, 26), 3: (74, 44), 4: (27, 51), 5: (78, 30), 6: (23, 30),
7: (20, 72), 8: (3, 27), 9: (5, 39), 10: (51, 1)}
# demands
d = {1: 302, 2: 273, 3: 275, 4: 266, 5: 287, 6: 296, 7: 297, 8: 310, 9: 302, 10: 309}
# plotting possible plant locations
for i, p in pf.items():
plt.scatter((p[0]), (p[1]), marker="^", color="purple", s=50)
plt.text((p[0]), (p[1]), "$f_%d$" % i)
# plotting location of clients
for i, p in pc.items():
plt.scatter((p[0]), (p[1]), marker="o", color="black", s=15)
plt.text((p[0]), (p[1]), "$c_{%d}$" % i)
plt.text((20), (78), "Region 1")
plt.text((70), (78), "Region 2")
plt.plot((50, 50), (0, 80))
dist = {(f, c): round(sqrt((pf[f][0] - pc[c][0]) ** 2 + (pf[f][1] - pc[c][1]) ** 2), 1)
for (f, c) in product(F, C) }
m = Model()
z = {i: m.add_var(ub=c[i]) for i in F} # plant capacity
# Type 1 SOS: only one plant per region
for r in [0, 1]:
# set of plants in region r
Fr = [i for i in F if r * 50 <= pf[i][0] <= 50 + r * 50]
m.add_sos([(z[i], i - 1) for i in Fr], 1)
# amount that plant i will supply to client j
x = {(i, j): m.add_var() for (i, j) in product(F, C)}
# satisfy demand
for j in C:
m += xsum(x[(i, j)] for i in F) == d[j]
# SOS type 2 to model installation costs for each installed plant
y = {i: m.add_var() for i in F}
for f in F:
D = 6 # nr. of discretization points, increase for more precision
v = [c[f] * (v / (D - 1)) for v in range(D)] # points
# non-linear function values for points in v
vn = [0 if k == 0 else 1520 * log(v[k]) for k in range(D)]
# w variables
w = [m.add_var() for v in range(D)]
m += xsum(w) == 1 # convexification
# link to z vars
m += z[f] == xsum(v[k] * w[k] for k in range(D))
# link to y vars associated with non-linear cost
m += y[f] == xsum(vn[k] * w[k] for k in range(D))
m.add_sos([(w[k], v[k]) for k in range(D)], 2)
# plant capacity
for i in F:
m += z[i] >= xsum(x[(i, j)] for j in C)
# objective function
m.objective = minimize(
xsum(dist[i, j] * x[i, j] for (i, j) in product(F, C)) + xsum(y[i] for i in F) )
m.optimize()
plt.savefig("location.pdf")
if m.num_solutions:
print("Solution with cost {} found.".format(m.objective_value))
print("Facilities capacities: {} ".format([z[f].x for f in F]))
print("Facilities cost: {}".format([y[f].x for f in F]))
# plotting allocations
for (i, j) in [(i, j) for (i, j) in product(F, C) if x[(i, j)].x >= 1e-6]:
plt.plot(
(pf[i][0], pc[j][0]), (pf[i][1], pc[j][1]), linestyle="--", color="darkgray"
)
plt.savefig("location-sol.pdf")
|
The allocation of clients and plants in the optimal solution is shown bellow. This example uses Matplotlib to draw the Figures.